Contact & Links
- Email: edwarddavis[at]hotmail.co.uk
- GitHub: edwarddavis1
- LinkedIn: edwarddavis941
- Google Scholar: Ed Davis
Professional Summary
I am a PhD graduate specialising in geometric deep learning and graph ML with 7+ years of Python development experience. T-shaped skill profile combining deep expertise in graph neural networks and uncertainty quantification with broad knowledge across AI/ML infrastructure, full-stack web development, and MLOps practices. Published researcher at top-tier ML conferences (ICLR 2025, UAI 2025). Recent open-source project experience includes building RAG systems with LangChain/ChromaDB, developing FastAPI applications with Websockets communication, and implementing comprehensive testing frameworks. Proven track record of translating research into real-world solutions across diverse industries, from healthcare systems at the NHS to insurance analytics at LV= (Allianz Group) and consulting research at the Smith Institute, demonstrating exceptional adaptability and cross-sector expertise.
Technical Skills
Programming Languages
Python, R, Bash, SQL, LaTeX, C++, JavaScript, HTML, CSS
Machine Learning & Deep Learning
PyTorch, PyTorch Geometric, JAX, Scikit-learn, LangChain, Hugging Face Transformers
Data Science & Visualisation
NumPy, SciPy, Pandas, Matplotlib, Seaborn, Plotly, D3.js
Web Development & APIs
FastAPI, WebSocket, Jinja2 Templating, Responsive Design
AI/ML Infrastructure
Retrieval-Augmented Generation (RAG), Vector Databases (ChromaDB), Semantic Search, Prompt Engineering
Software Development
GitHub, Unit Testing, pytest, Mock Testing, Coverage Testing, CI/CD, GitHub Actions, Pre-commit Hooks, Code Linting (Ruff), Sphinx, Linux, Docker
Research Papers
Valid Conformal Prediction for Dynamic GNNs (ICLR 2025)
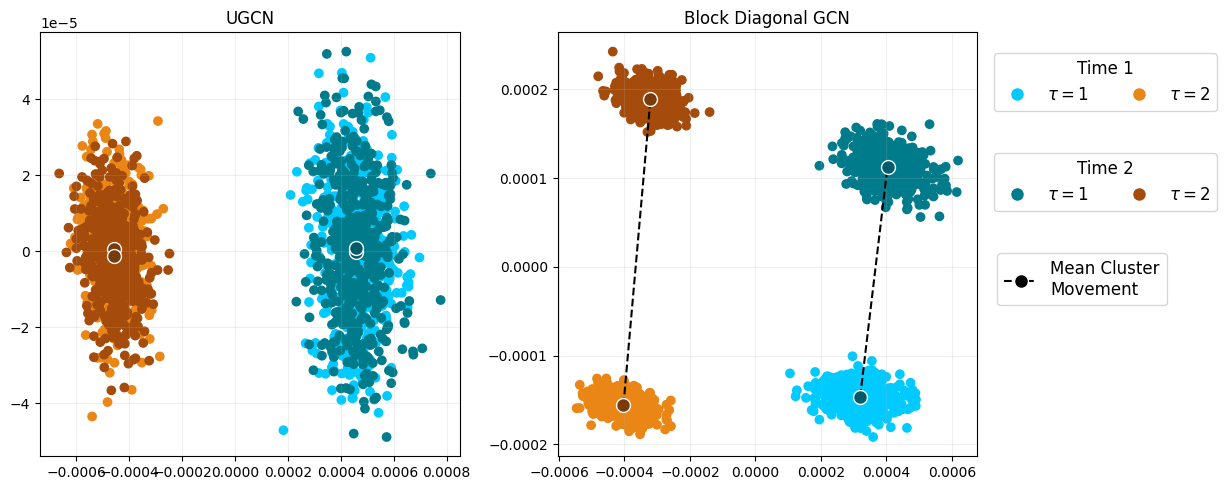
A Simple and Powerful Framework for Stable Dynamic Network Embedding (Preprint)
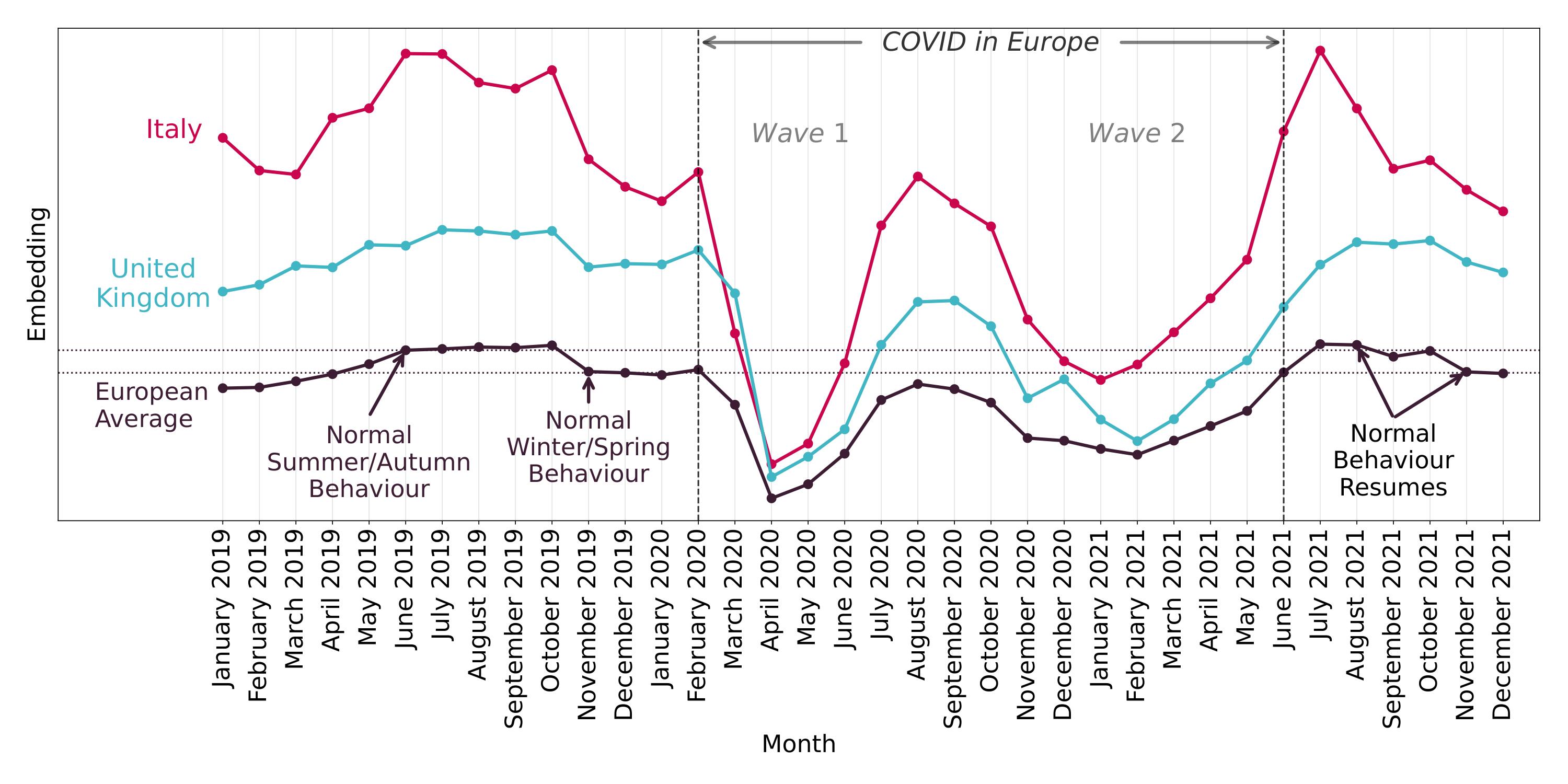
Valid Bootstraps for Networks with Applications to Network Visualisation (UAI 2025)
Recent Projects
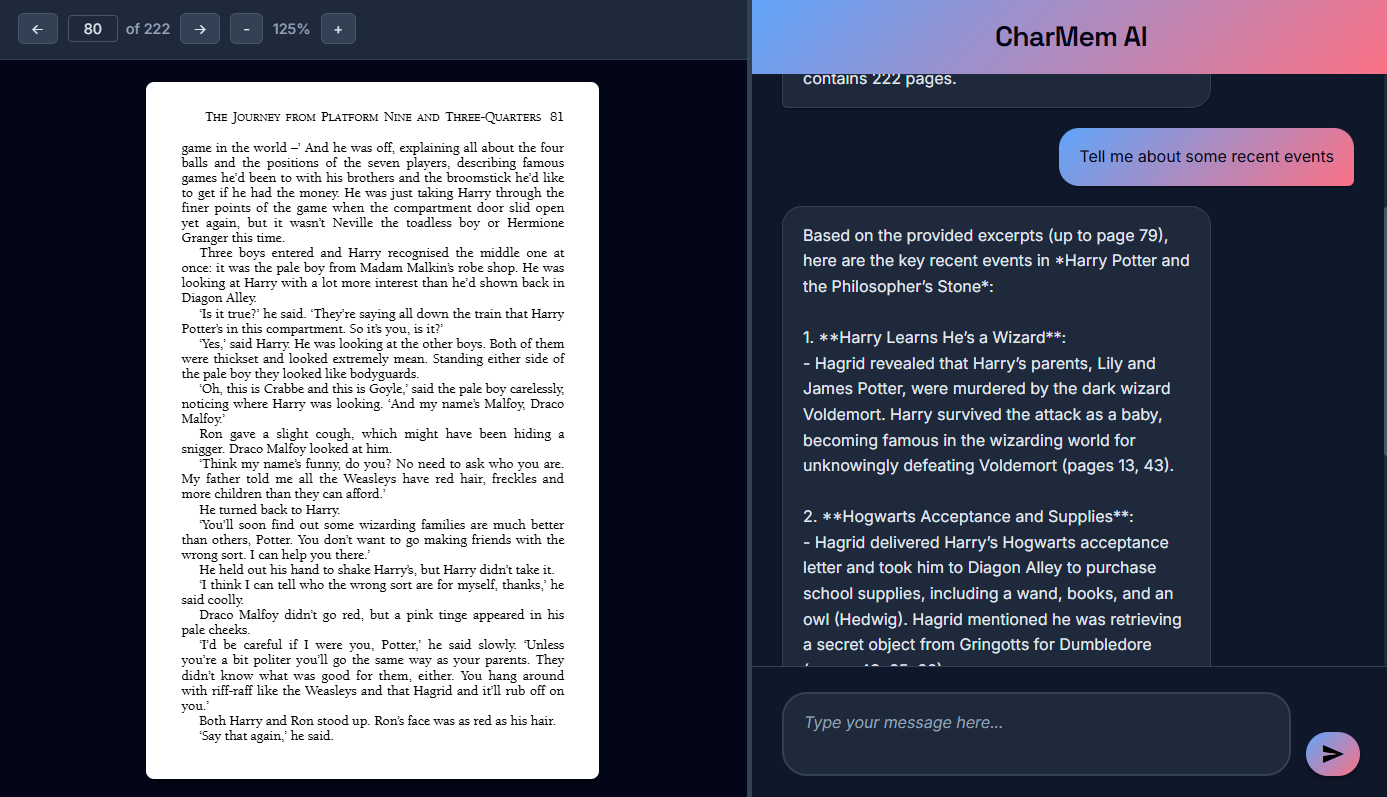
CharMem - AI Character Memory Assistant
CharMem is an intelligent chat application that helps readers keep track of characters in books using retrieval-augmented generation (RAG) with anti-spoiler technology. Upload any PDF book and get instant character summaries with page references - without spoilers!
Features include PDF upload & processing, anti-spoiler conversations, AI-powered responses using Qwen-235B model, real-time WebSocket chat, and precise page references for character introductions.
# CharMem programmatic usage
from backend.RAG import EmbeddedPDF
from langchain.document_loaders import PyPDFLoader
# Load your PDF
loader = PyPDFLoader("path/to/your/book.pdf")
pages = loader.load()
# Create embedder and process PDF
pdf_embedder = EmbeddedPDF()
pdf_embedder.embed_pdf(pages)
# Query character information
response = pdf_embedder.generate_character_analysis("Character Name")
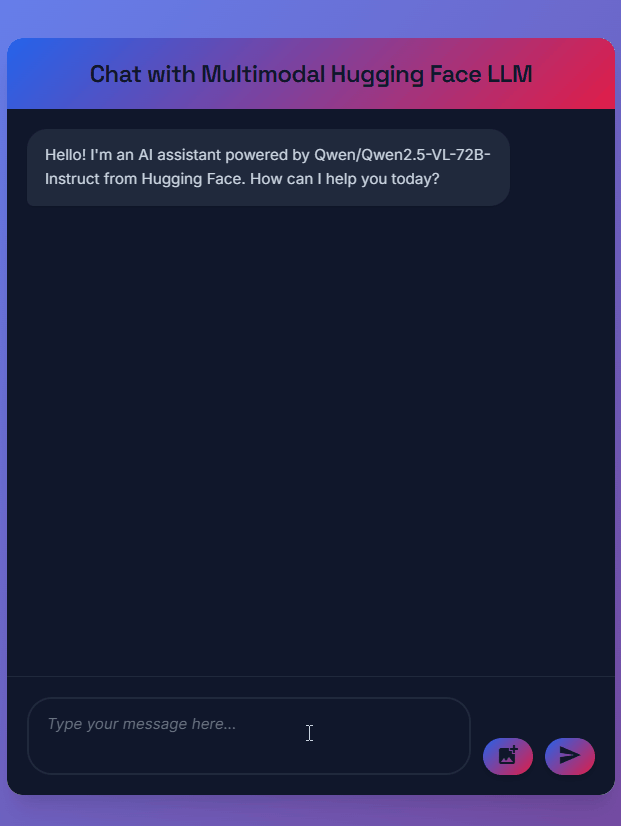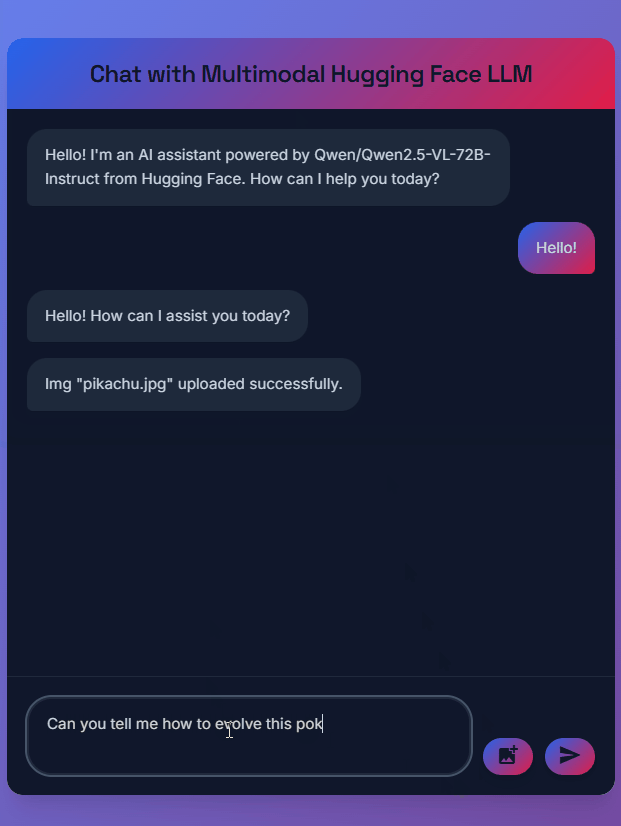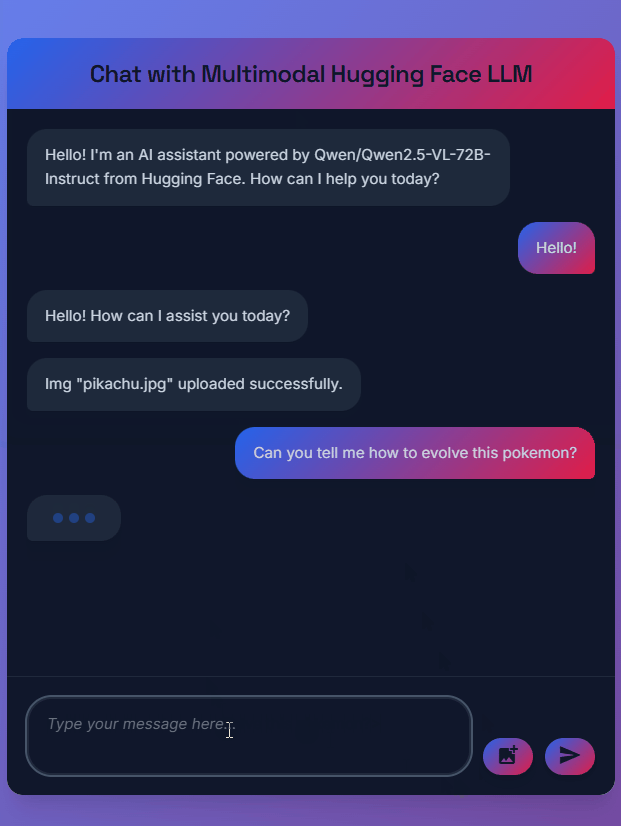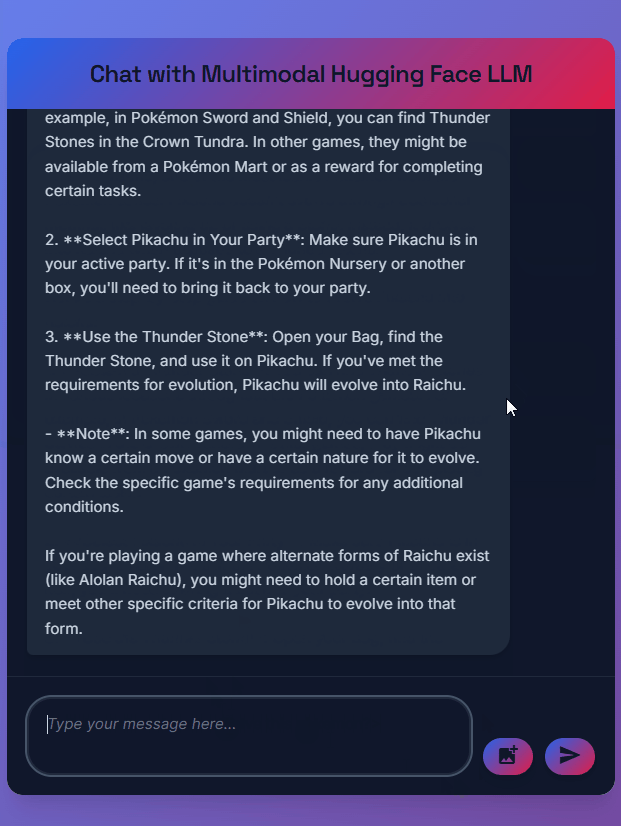
print(response)Multimodal Chatbot with FastAPI
A web application that enables real-time chat with Large Language Models using Hugging Face's Inference Providers system. Built with FastAPI backend and modern JavaScript frontend, featuring WebSocket communication and multimodal capabilities.
The chatbot supports both text and image inputs, uses models like Qwen2.5-VL-72B-Instruct for vision capabilities, and features a responsive dark-themed interface with smooth animations and typing indicators.
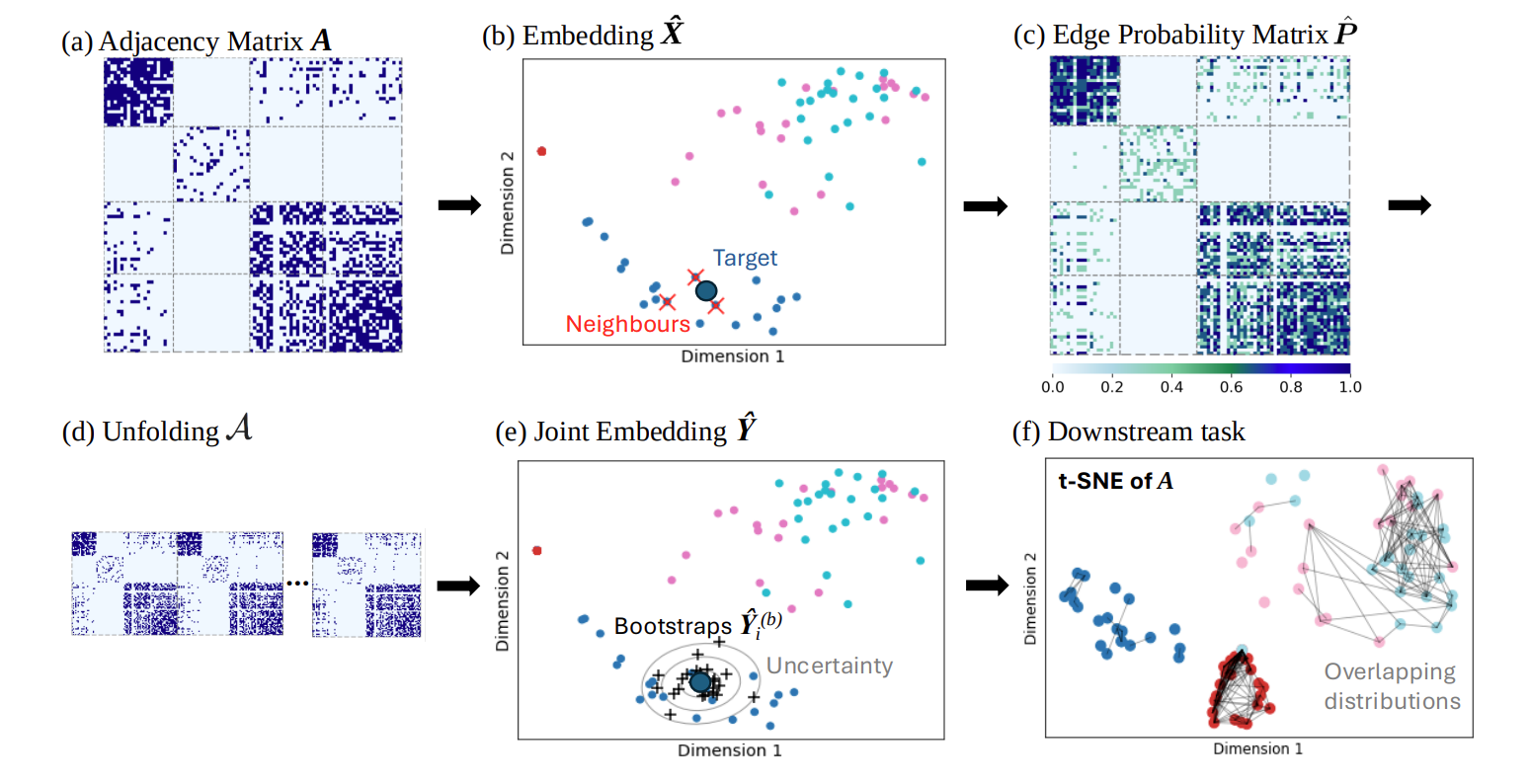
A PyTorch implementation of the unfolded graph neural network (UGNN), a powerful and interpretable model for multi-network prediction.
The model has a theoretical guarantee of valid conformal prediction when predicting into the future on many datasets. Conformal prediction allows for a range of predictions to be output from a single model for the purpose of uncertainty quantification, no matter if the model is a black-box or not. Below is an example of conformal node prediction, which is valid under a UGNN.
# UGNN model output
output = best_model(unf_network.x, unf_network.edge_index, unf_network.edge_weight)
# Apply conformal prediction (for uncertainty quantification)
all_pred_sets = get_prediction_sets(
output, unf_network, calib_mask, test_mask, score_function="APS", alpha=0.1
)# Look at the prediction sets for 10 random nodes
for calib_node_idx in np.random.randint(len(all_pred_sets), size=10):
node_pred_set = all_pred_sets[calib_node_idx]
node_idx = np.where(calib_mask == 1)[0][calib_node_idx]
possible_labels_for_node = [
str(all_labels[pred]) for pred in np.where(node_pred_set == 1)[0]
]
print(
f"Node {node_idx} (True label {str(all_labels[unf_network.y[node_idx]])}): {possible_labels_for_node}"
)Node 4352 (True label Teachers): ['1A', '1B', '2A', '2B', '3A']
Node 3657 (True label 1B): ['1A']
Node 4162 (True label 2A): ['1B', '2A', '2B']
Node 3492 (True label 3A): ['1A', '1B', '2A', '3A', '3B']
Node 3675 (True label 1B): ['1A', '1B', '2A']
Node 3095 (True label 5A): ['4A', '4B', '5B']
Node 3097 (True label 5A): ['4A', '5A']
Node 3704 (True label 2B): ['1A', '2A', '2B', '3A']
Node 2941 (True label 1B): ['1A', '1B', '4A']
Node 3704 (True label 2B): ['1A', '2A', '2B', '3A']A Python package for exploring complex datasets including high-dimensional data, relational databases and networks.
For example, the below code can quickly compute a URLSE dynamic embedding and then produce an interactive plot of the embedding over time.
import pyemb as eb
# Embed the graph using unfolded regularised Laplacian spectral embedding
d = 10
URLSE_emb = eb.dyn_embed(As, d=d, method="URLSE")
# Quick interactive + animated plot of the embedding
fig = eb.quick_plot(URLSE_emb, n, T, node_labels)Example Interactive Visualisation:
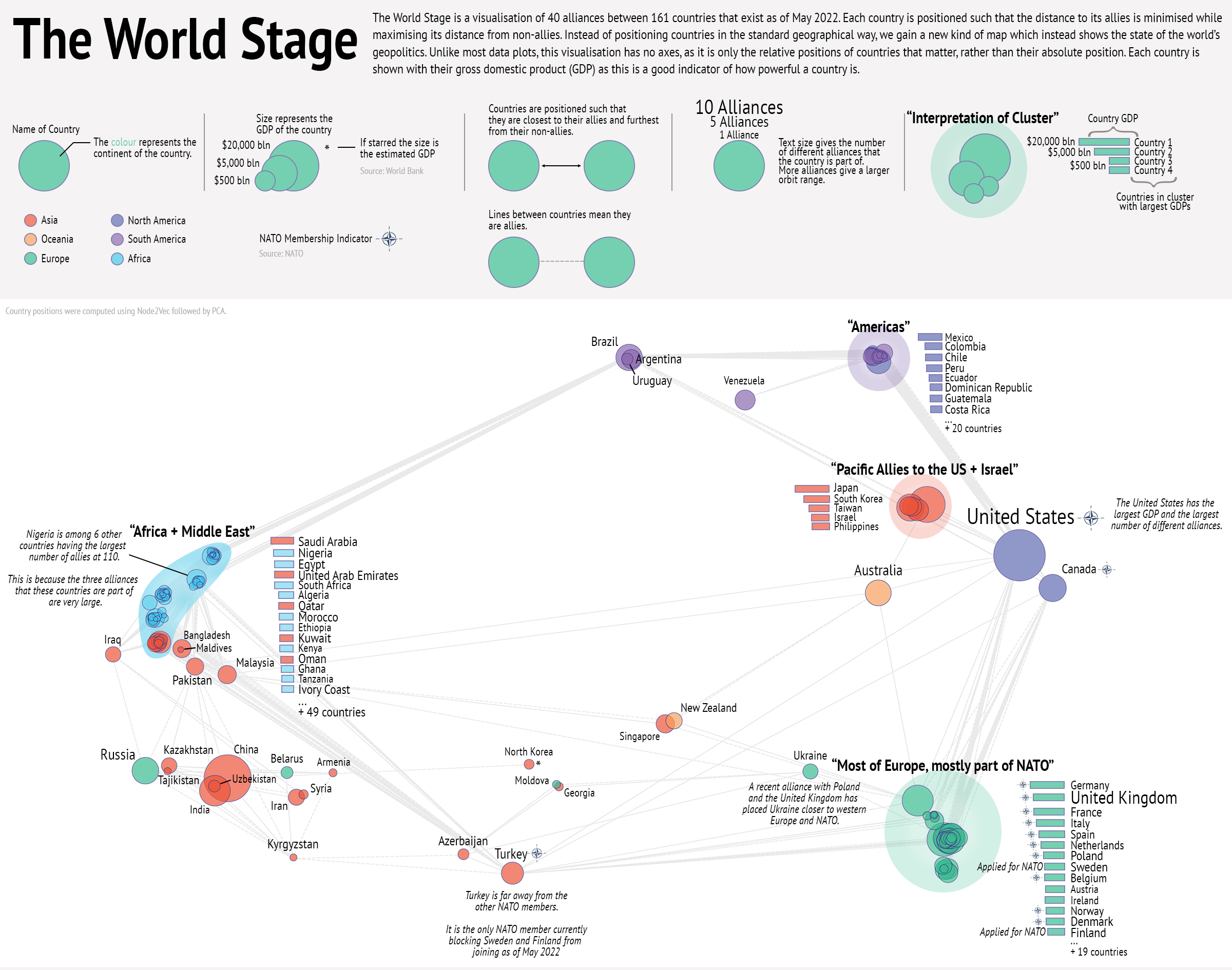
Award-Winning Data Visualisation
Runner-up in the Jean Golding Institute's Beauty of Data competition. This visualisation was presented at the Bristol Data and AI Showcase 2022.
This visualisation displays an embedding of a friendship network between countries on the world stage based on their alliances.